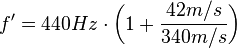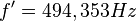Umbral del dolor

El término umbral del dolor refiere a la intensidad o a la duración máxima de un sensorial estímulo en cuál cierra el cuerpo. En literatura científica el término se distingue claramente del término tolerancia del dolor. Umbral del dolor es el estímulo mínimo que saca dolor y lo implica medida del estímulo intensidad, mientras que tolerancia del dolor es el grado de dolor que un tema puede tolerar, e implica a medida de la respuesta de un tema al dolor.

Ejemplo

Considere, como ejemplos, los tres estímulos potencialmente dolorosos del calor aplicados a la piel, la presión en un hueso del shin, o la interrupción de la fuente de la sangre a un músculo. Cuando están solicitados en la intensidad reducida, o un a corto plazo, estos acontecimientos se reconocen como sensaciones no-dolorosas. Progresivamente intensificando o prolongando el estímulo, una etapa es alcanzada donde el tema/la persona diría que “eso es dolorosa”, o, en el caso de animales, cuando ocurre una cierta respuesta observable que se presume para ser indicativa de dolor. La temperatura, la presión, o la duración de la isquemia del músculo en la cual ese cambio de la sensación ordinaria al dolor ocurre, es el dolor que umbral-es una medida del estímulo cuando ocurre la respuesta, pero no una medida de la respuesta. En los casos mencionados el umbral del dolor puede ser expresado como los grados centígrados, los kilopascals, o segundos respectivamente. El uso de tales unidades indica claramente el significado del término, como no una medida de “lastimó” o “sufriendo”.

Umbral creciente y disminuido del dolor

El umbral del dolor es sobre todo una función de cómo es sano son los nervios del dolor y el dolor central que procesan caminos, y del entorno químico en los tejidos finos que el innervate de los nociceptors. Se reduce comúnmente cercainflamación en la vecindad de nociceptors, tales que el tacto normal llega a ser doloroso en el área de la inflamación (allodynia). En tales circunstancias, el uso de medicaciones antiinflamatorias o las terapias físicas tales como refrescarse o calor suave pueden volver la sensibilidad o el umbral del nervio a normal - no aumenta el umbral a normal antedicho.

El uso de morfina- como las drogas eleva el umbral del dolor (así como tolerancia del dolor). Igual es verdad de un número diverso de otro centralmente actuar analgesia drogas que afectan las neuronas del relais del dolor. Las técnicas físicas locales tales como estímulo, refrescarse o calor eléctrico pueden aumentar temporalmente el umbral del dolor.

Sin embargo, corto de los nervios perjudiciales del dolor - tales como puede ocurrir adentro nervio lesiones o neuropathies - los efectos de intervenciones (farmacológico o la comprobación) usada para aumentar el umbral del dolor no dura mucho más de largo que la duración de su uso. Además, en personas sanas normales, no es cambiado perceptiblemente por ninguna práctica o entrenamiento mental o física. En cambio, tolerancia del dolor puede ser aumentado en las medicaciones así como por intervenciones y el entrenamiento físicos, cognoscitivos y afectivos.

umbral de audicion

Umbral de audición .

El umbral de audición es la intensidad mínima de sonido capaz de impresionar el oído humano. Aunque no siempre este umbral sea el mismo para todas las frecuencias que es capaz de percibir el oído humano, es el nivel mínimo de un sonido para que logre ser percibido.

El valor normal se sitúa entre 0 dB audiométrico, equivalentes a 20 micropascales y 25 dB audiométricos, sin embargo, en frecuencias muy bajas, como aproximados a los 20 Hz hasta los casi 80 Hz. Este Umbral tiende a subir debido a que estas frecuencias poseen un sonido mucho más bajo. Caso contrario sucede en las frecuencias superiores a las 10.000 Hz; pues debido a la agudez de estas ondas el umbral de 0 siempre es este.

Los 0 dB se expresan en Intensidad como 10^-12 [Watts/m²] y en variación de la presión como 2·10^-5 [N/m²].

Velocidad del sonido.

La velocidad del sonido es la velocidad de propagación de las ondas mecánicas longitudinales, producidas por variaciones de presión del medio. Estas variaciones de presión generan en el cerebro la sensación del sonido.

La velocidad de propagación de la onda sonora depende de las características del medio en el que se realiza dicha propagación y no de las características de la onda o de la fuerza que la genera.

La velocidad del sonido es importante, porque nos da una medida del tiempo mínimo en que una variación de presión puede transmitirse desde un punto a otro. Las ondas de comprensión de sólidos y líquidos se llaman también ondas sonoras.  

La velocidad del sonido varía también ante los cambios de temperatura del medio. Esto se debe a que un aumento de la temperatura se traduce en un aumento de la frecuencia con que se producen las interacciones entre las partículas que transportan la vibración, y este aumento de actividad hace aumentar la velocidad.

La definición termodinámica de la velocidad del sonido, para cualquier medio,  es a²=(dp/dρ)s es decir la derivada parcial de la presión con respecto de la densidad a entropía constante. Por ejemplo, sobre una superficie nevada el sonido es capaz de desplazarse atravesando grandes distancias. Esto es posible gracias a las refracciones producidas bajo la nieve, que no es un medio uniforme. Cada capa de nieve tiene una temperatura diferente. Las más profundas, donde no llega el sol, están más frías que las superficiales. En estas capas más frías próximas al suelo, el sonido se propaga con menor velocidad.
En general, la velocidad del sonido es mayor en los sólidos que en los líquidos y en los líquidos es mayor que en los gases. Esto se debe al mayor grado de cohesión que tienen los enlaces atómicos o moleculares conforme más sólida es la materia.

Velocidad del sonido en los gases

En los gases la ecuación de la velocidad del sonido es la siguiente:

Siendo γ el coeficiente de dilatación adiabática, R la constante universal de los gases, T la temperatura en kelvin aguas arriba de la perturbación y M la masa molar del gas.

Velocidad del sonido en los sólidos

En sólidos la velocidad del sonido está dada por:

donde E es el módulo de Young y ρ es la densidad. De esta manera se puede calcular la velocidad del sonido para el acero, que es aproximadamente de 5.148 m/s.

Velocidad del sonido en los líquidos.

La velocidad del sonido en el agua es de interés para realizar mapas del fondo del océano. En agua salada, el sonido viaja a aproximadamente 1.500 m/s y en agua dulce a 1.435 m/s. Estas velocidades varían principalmente según la presión, temperatura y salinidad.

Efecto Doppler

El efecto Doppler, llamado así por el austríaco Christian Andreas Doppler. Doppler propuso este efecto en 1842 en su tratado. Sobre el color de la luz en estrellas binarias y otros astros).

El científico neerlandés Christoph Hendrik Diederik Buys Ballot investigó esta hipótesis en 1845 para el caso de ondas sonoras y confirmó que el tono de un sonido emitido por una fuente que se aproxima al observador es más agudo que si la fuente se aleja. Hippolyte Fizeau descubrió independientemente el mismo fenómeno en el caso de ondas electromagnéticas en 1848. En Francia este efecto se conoce como "efecto Doppler-Fizeau" y en los Países Bajos como el "efecto Doppler-Gestirne".

El Efecto Doppler se observa en ondas de todo tipo (ondas sonoras, ondas electromagnéticas, etc.).

El efecto Doppler se aprecia cuando una fuente de ondas se mueve.

 

Ejemplo

Un observador se mueve a una velocidad de 42 m/s hacia un trompetista en reposo. El trompetista está tocando (emitiendo) la nota La (440 Hz). ¿Qué frecuencia percibirá el observador, sabiendo que = 340 m/s

Solución: Si el observador se acerca hacia la fuente, implica que la velocidad con que percibirá cada frente de onda será mayor, por lo tanto la frecuencia aparente será mayor a la real (en reposo). Para que esto ocurra debemos aplicar el signo (+) en la ecuación.

Christian Andreas Doppler nació el 29 de noviembre de 1803 en Salzburgo, Austria, en el seno de una próspera familia burguesa dedicada desde 1674 a los negocios. Debido a su frágil salud no siguió la tradición familiar. Realizó los estudios primarios en Salzburgo y los secundarios en Linz. Pronto llegó a manifestar un especial talendo para las matemáticas y, por consejo de uno de sus profesores del liceo, ingresó en el Instituto Politécnico de Viena, que se había fundado en 1815. Allí permaneció entre 1822 y 1825, año en el que se graduó. Regresó a Salzburgo y, poco después, continuó sus estudios en la Universidad de Viena, mostrando especial interés en materias como la astronomía, mecánica y matemáticas avanzadas. Cuando terminó sus estudios, en 1929, fue contratado como asistente del profesor Burg, cuya especialidad era la mecánica y las matemáticas. Durante los cuatro años que estuvo ocupando este puesto publicó cuatro artículos de tema matemático.

Trate de recordar el sonido de una sirena cuando se mueve en su dirección y luego pasa. Los sonidos cambian. Este cambio se explica a través del Efecto Doppler. Las ondas de sonido que se mueven hacia usted son ondas comprimidas, mientras que las ondas que pasan, están extendidas. Esto sucede con muchos tipos de ondas.

 Podemos comprobar que el efecto Doppler se debe al movimiento relativo del observador con respecto al emisor, haciendo que el observador y el emisor se muevan con la misma velocidad y en la misma dirección. Medimos el tiempo que tarda en pasar por el emisor, dos frentes de ondas consecutivos, y lo comparamos con el periodo de las ondas emitidas (una unidad de tiempo).

Pulsaciones

La superposición de ondas de frecuencias ƒ1 y ƒ2 muy cercanas entre sí produce un fenómeno particular denominado pulsación (o batido).En esos casos nuestro sistema auditivo no es capaz de percibir separadamente las dos frecuencias presentes, sino que se percibe una frecuencia única promedio (ƒ1 + ƒ2) / 2, pero que cambia en amplitud a una frecuencia de ƒ2 - ƒ1 . Es decir, si superponemos dos ondas senoidales de 300 Hz y 304 Hz, nuestro sistema auditivo percibirá un único sonido cuya altura corresponde a una onda de 302 Hz y cuya amplitud varía con una frecuencia de 4 Hz (es decir, cuatro veces por segundo). Las pulsaciones se perciben para diferencias en las frecuencias de hasta aproximadamente 15-20 Hz. Diferencias mayores de 15-20 Hz le dan al sonido percibido un carácter áspero, mientras que si la diferencia aumenta comienzan nuevamente a percibirse las dos ondas simultánea y separadamente.

el decibel y tono

El decibelio, cuyo símbolo es dB, es una unidad logarítmica. Es un submúltiplo del belio, de símbolo B, que es el logaritmo de la relación entre la magnitud de interés y la de referencia, pero no se utiliza por ser demasiado grande en la práctica, y por eso se utiliza el decibelio, la décima parte de un belio. El belio recibió este nombre en honor de Alexander Graham Bell. Un belio equivale a 10 decibelios y representa un aumento de potencia de 10 veces sobre la magnitud de referencia. Cero belios es el valor de la magnitud de referencia. Así, dos belios representan un aumento de cien veces en la potencia, 3 belios equivalen a un aumento de mil veces y así sucesivamente.

El tono de un sonido aumenta con la frecuencia, pero no en la misma medida. Con la frecuencia lo que medimos es el número de vibraciones. Su unidad de medida es el herzio (Hz). Para expresar una frecuencia lo hacemos refiriéndonos a vibraciones por segundo. Así un frecuencia de 1 Herzio es lo mismo que decir que el sonido tiene una vibración por segundo.